Las magnitudes físicas pueden ser:
- Magnitudes escalares. Son aquellas que quedan perfectamente definidas con su unidad correspondiente y una determinada cantidad (tiempo, temperatura, masa, densidad etc)
- Magnitudes vectoriales. Son aquellas que para quedar definidas se debe conocer la cantidad, la unidad, la dirección y el sentido (fuerza, acerelación, velocidad, campo electrico etc)
 Las magnitudes fundamentales son aquellas magnitudes a partir de las cuales se obtienen todas las demás. en la siguiente se recogen estas magnitudes con su unidad segun el Sistema Internacional de Medidas.
Las magnitudes fundamentales son aquellas magnitudes a partir de las cuales se obtienen todas las demás. en la siguiente se recogen estas magnitudes con su unidad segun el Sistema Internacional de Medidas.Todas las demás magnitudes son derivadas, ya que se obtinen por combinación de las anteriores. Un pequeño ejemplo de estas magnitudes son:

La Física, como toda ciencia experimental, se basa en la toma de datos, es decir de medidas. Para reducir las posibilidades de error al máximo, en los laboratorios nunca se realiza una sola medida de una variable, sino varias, de las cuales se obtiene una srie de datos que luego se tratan matemáticamente.
Valor real de una medida
Dado un conjunto de medidas
consideramos el valor de la medida como la media aritmética de las medidas del conjunto:
Error absoluto
consideramos el valor de la medida como la media aritmética de las medidas del conjunto:
Error absoluto
Es la diferencia máxima entre el valor de cada medida y la media aritmética de las medidas; se mide en la misma unidad que la magnitud.
Error relativo
Error relativo
Es el cociente que se obtiene de dividir el error absoluto ( multiplicado por 100) por la media aritmetica de las medidas. No tiene unidades y se expresa como % de error.
Valor de una medida con sus errores
Cálculo vectorial
Un vector es un segmento orientado. Sus componentes son:- Dirección, que es la recta sobre la que se aplica el vector.
- Sentido, que viene indicado por la flecha.
- Módulo, que es la longitud del segmento. Representa la intensidad de las magnitudes vectoriales.
- Punto de aplicación, que es el origen del vector.
Un vector también se puede representar en forma polar, teniendo en cuenta el módulo del vector y el ángulo que forma con el eje de abscisas.
El método científico
El método científico es el conjunto de procesos o etapas que intervienen en la obtención de un determinado conocimiento científico. las principales etapas son las siguientes:
1. Planteamiento del problema con precisión. se
basa en la observación sistemática del fenómeno que se desea estudiar.
2. Propuesta de hipótesis. las hipótesis son las
suposiciones provisionales que se establecen sobre las causa del fenómeno.
3.
Comprobación experimental de las hipótesis. se
repite el fenómeno en circunstancias adecuadas, controlando las variables (
factores que intervienen en los resultados del experimento) e intentando
averiguar la influencia que tienen en el fenómeno.
4.
Análisis de los datos recogidos en los
experimentos y formulación de una ley. Se trata de establecer la relación entre
los datos. la relación hallada se denomina ley, que, por lo general, se expresa
en forma de ecuación matemática. Varias leyes que explican diferentes aspectos
de un mismo fenómeno forman una teoría.
Los datos en tablas. interpretación de graficas.
·
El estudio de cualquier fenómeno obliga a
seleccionar las variables que intervienen en él. Son variables la masa, el
volumen, la longitud, la presión, el tiempo, el espacio...
·
Después se construye una tabla de datos, en la
que se ordenan en filas y columnas los valores numéricos de las diferentes
variables que intervienen en el fenómeno. A la variable modificada regularmente
se la llama independiente, la otra variable recibe el nombre de dependiente.
·
La mejor manera de encontrar una relación entre
las dos variables es la representación gráfica. Cuando se ha representado todos
los valores, se traza la línea de ajuste, que muestra la tendencia general de
la distribución de dichos valores. puede ser una recta o una curva.
o
Si la línea
de ajuste es una recta, las dos variables cumplen la relación y= mx + n donde m
representa el punto de corte de la recta con el eje Y, y m es la pendiente de
la recta.
o
Si la línea de ajuste es una curva, las dos
variables pueden una de estas dos relaciones: y =ax2 o
y=a/x según se trate de una parábola
o una hipérbola, respectivamente.

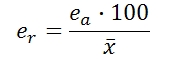





No hay comentarios:
Publicar un comentario